Tolerances: tradeoff: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
|- valign="top" | |- valign="top" | ||
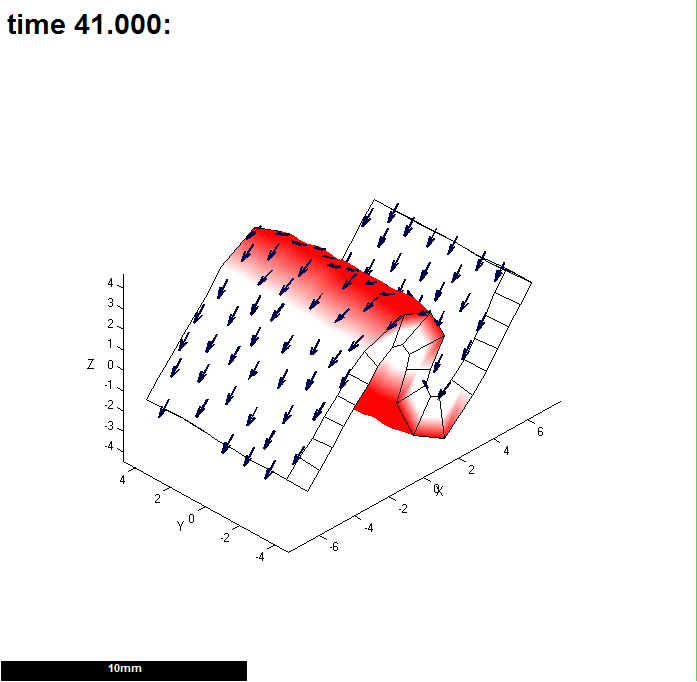
|width="200px"|[[File:GPT_DemoTol1.png|200px|GFtbox interface]]Tolerance (Tol Elast) is 0.1. '''Is the 'S' shape correct?'''<br><br> Simple mesh of 382 elements equally spaced vertices. Superimposed are the polarity arrows (pointing bottom left) and purple and blue factors that control local growth rates. | |width="200px"|[[File:GPT_DemoTol1.png|200px|GFtbox interface]]Tolerance (Tol Elast) is 0.1. '''Is the 'S' shape correct?'''<br><br> Simple mesh of 382 elements equally spaced vertices. Superimposed are the polarity arrows (pointing bottom left) and purple and blue factors that control local growth rates. | ||
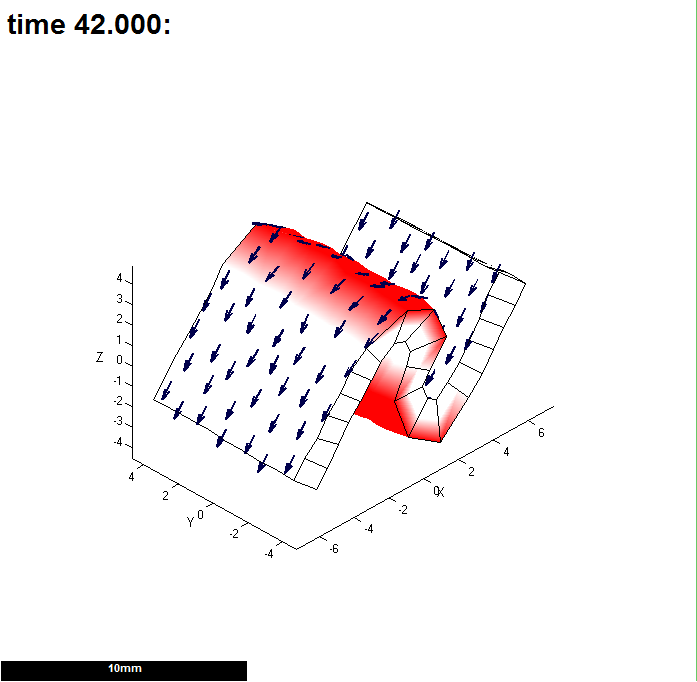
|width="200px"|[[File: | |width="200px"|[[File:GPT_DemoTol2.png|200px|GFtbox interface]]Tolerance (Tol Elast) is 0.001. '''Is the 'S' shape correct?''' It is different so we reduce it again... | ||
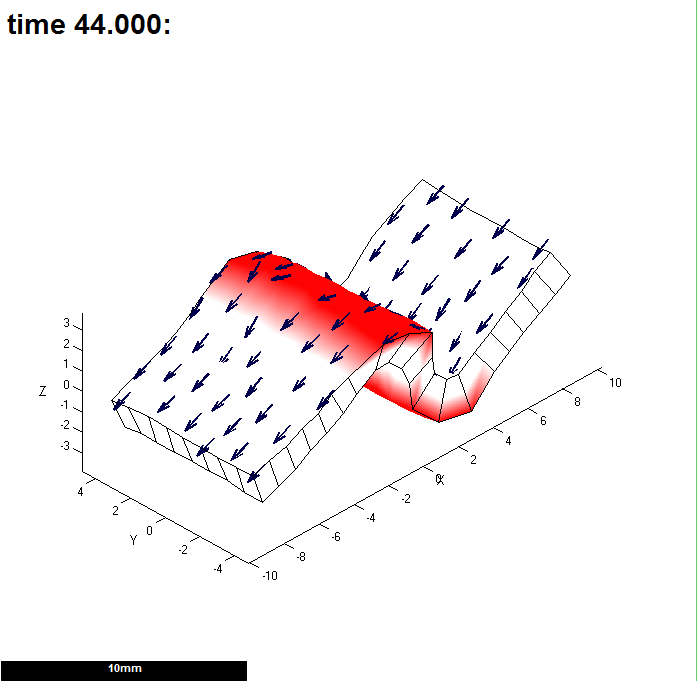
|width="200px"|[[File:GPT_DemoTol3.png|200px|GFtbox interface]]Tolerance (Tol Elast) is 0.00001. This shape is very similar to the previous one so we might conclude that it is not necessary to make the tolerance this tight, a tolerance of 0.001 is OK. | |width="200px"|[[File:GPT_DemoTol3.png|200px|GFtbox interface]]Tolerance (Tol Elast) is 0.00001. This shape is very similar to the previous one so we might conclude that it is not necessary to make the tolerance this tight, a tolerance of 0.001 is OK. | ||
|} | |} | ||
Revision as of 12:40, 6 December 2012
Return to GFtbox hints and tips
Choosing tolerances that are small enough to be accurate and yet not take too long to compute
There is a tradeoff between speed and the accuracy with which the equation solver can solve the equations. This is feature of all numerical modelling. The solver attempts to reduce errors to zero. It is extremely unlikely to succeed so there are two mechanisms to truncate calculations after a reasonable time. The number of iterations and a maximum error that is deamed satisfactory, i.e. the tolerance. There are two tolerances one for diffusion (which usually does not need to be changed) and the second for the mesh. A large tolerance means that the mesh might not have deformed as much as it should. A tight tolerance means that it takes longer (but sometimes it actually takes less time as fine detail can be resolved so starting the next iteration from a better place). This is an example of subdividing a rectangular mesh in the region in which curves will develop.
It still might not be correct because the mesh itself could be too coarse, see mesh tradeoffs
It still might not be correct because the timesteps might be too large, see time tradeoffs