One dimensional sieve applied to images: Difference between revisions
Jump to navigation
Jump to search
| Line 38: | Line 38: | ||
{| border="0" cellpadding="5" cellspacing="5" | {| border="0" cellpadding="5" cellspacing="5" | ||
|- valign="top" | |- valign="top" | ||
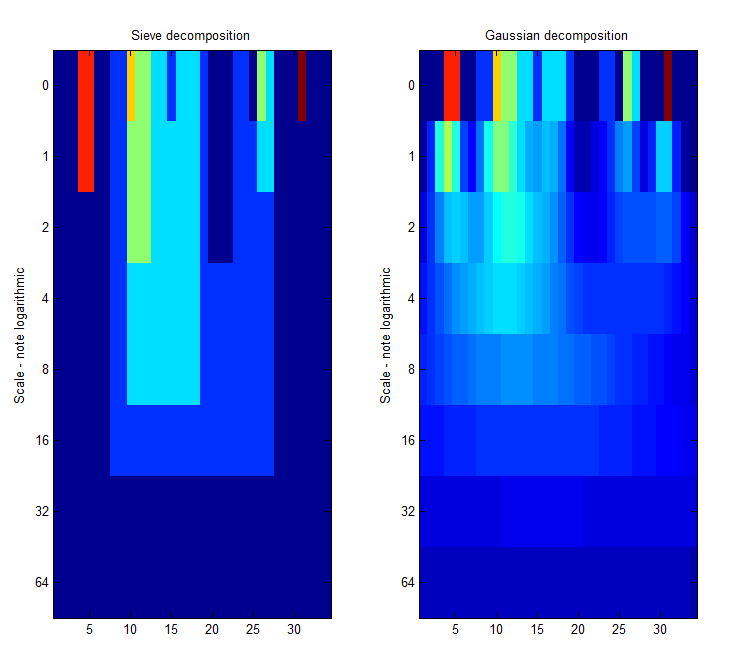
|width="50%"| Left Panel. '''A low-pass''' 'm' sieve can remove extrema at multiple scales. Here, siv4.m gradually removes extrema as scale increases from scale 1 to scale 64. The resulting traces are shown as a 'heat map' where the signal goes from left to right, bright colours like red are large amplitude, small scale extrema. At each increasing scale (down the map) smaller scale extrema have been removed. As result, we can for example see the buried large scale, low amplitude pulse revealed in panel 4 of the previous Figure, as a light green rectangle that starts at ''n=6'' and persists to ''n=26'', i.e. ''scale= | |width="50%"| Left Panel. '''A low-pass''' 'm' sieve can remove extrema at multiple scales. Here, siv4.m gradually removes extrema as scale increases from scale 1 to scale 64. The resulting traces are shown as a 'heat map' where the signal goes from left to right, bright colours like red are large amplitude, small scale extrema. At each increasing scale (down the map) smaller scale extrema have been removed. As result, we can for example see the buried large scale, low amplitude pulse revealed in panel 4 of the previous Figure, as a light green rectangle that starts at ''n=6'' and persists to ''n=26'', i.e. ''scale=20''. <br><br> | ||
The 'm'-sieve preserves scale-space so no new extrema (light regions) are formed as we move to increasing scales. Right Panel. A ''Gaussian'' filter bank also preserves scale-space as shown by Witkin 1986. | |||
|[[Image:Siv4 test 5.png|400px|'m' non-linear filter (sieve) compared to Gaussian filter]] | |[[Image:Siv4 test 5.png|400px|'m' non-linear filter (sieve) compared to Gaussian filter]] | ||
|} | |} | ||
Revision as of 15:09, 19 June 2014
'siv4.mex' implemenation applies the m-sieve to a vector or column wise to a matrix
A Matlab function siv4_test.m illustrates how siv4.mex can be used to analyse columns of 1D data.
Consider a signal, <math>X</math>X=getData('PULSES3WIDE')
>blue X=0 5 5 0 0 1 1 4 3 3 2 2 1 2 2 2 1 0 0 0 1 1 0 3 2 0 0 0 6 0 0
|
| The data has minima and maxima of different scales (lengths). In one dimension we measure pulse length using a ruler, measuring tape or whatever - but not frequency or Gaussian scale. | 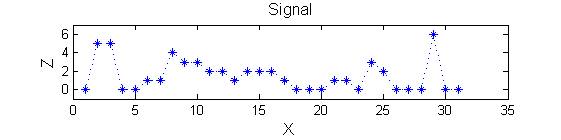
|
Filter
Lowpass siv4.mex
data{1}=siv4_alt('PULSES3WIDE',[2;5;10]);
data{1}
ans =
y: {[34x1 double] [34x1 double] [34x1 double]} % outputs for the 3 specified scales
scan: [34 34] % instructing single column processing
X: [34x1 double] % input data
options: [3x4 double] % options (see elsewhere)
outputs: 'lll' % outputs all lowpass
type: 'int' % input data may be double but only contains integers
name: 'PULSES3WIDE'
Now think about scale-space.
scaleA=1; Y1=SIVND_m(X,scaleA,'o');
scaleB=2; Y2=SIVND_m(X,scaleB,'o');
red=double(X)-double(Y1); green=double(Y1)-double(Y2);
Repeat over scales 0 to 15
| Increasing the scale (towards the front) removes extrema of increasing length. The algorithm cannot create new maxima (it is an 'o' sieve) it is, therefore, scale-space preserving. | 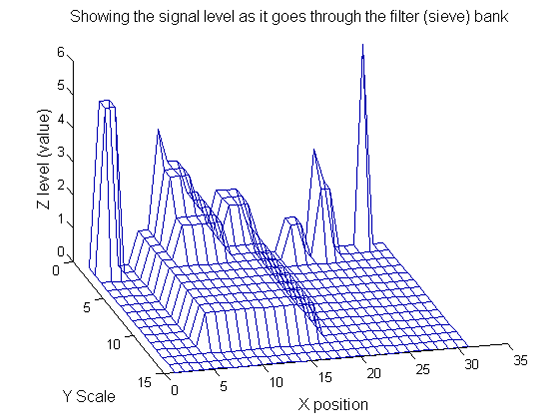
|
YY=ones([length(X),1+maxscale]);
for scale=0:maxscale
Y2=SIVND_m(Y1,scale,'o',1,'l',4);
YY(:,scale+1)=Y2';
Y1=Y2; % each stage of the filter (sieve) is idempotent
end
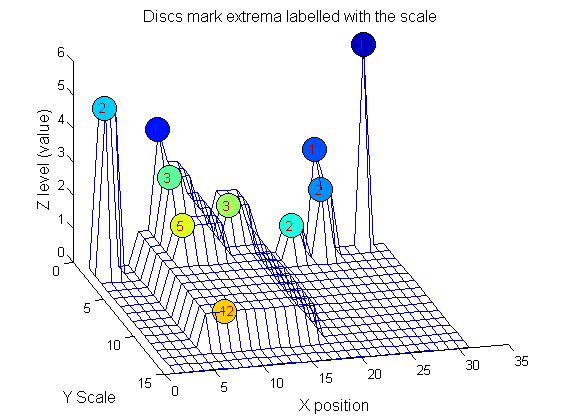
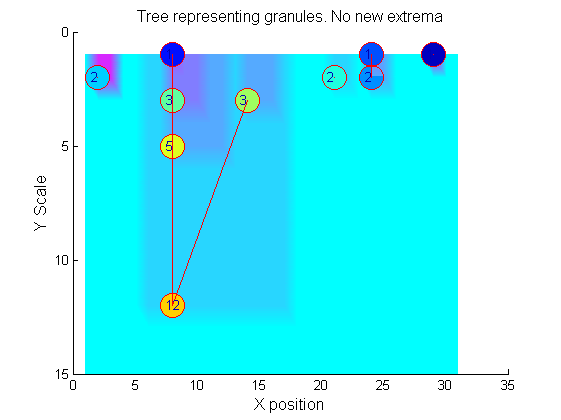
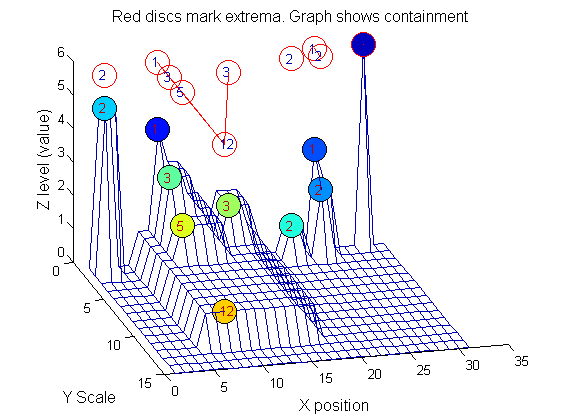
Label the granules
g=SIVND_m(X,maxscale,'o',1,'g',4);
g = Number: 10
area: [1 1 1 2 2 2 3 3 5 12]
value: [6 1 1 2 5 1 1 1 1 1]
level: [6 4 3 2 5 1 3 2 2 1]
deltaArea: [5 2 1 7 3 12 2 2 7 19]
last_area: [6 3 2 9 5 14 5 5 12 31]
root: [29 8 24 24 2 21 8 14 8 8]
PictureElement: {1x10 cell}
g.PictureElement
Columns 1 through 9
[29] [8] [24] [2x1 double] [2x1 double] [2x1 double] [3x1 double] [3x1 double] [5x1 double] [12x1 double]
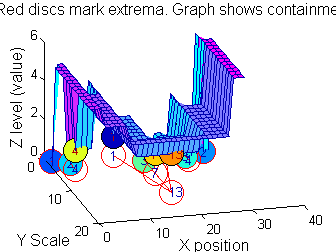
Tracing the granules through scale-space identifies candidate MSER's
We have candidate 1D MSER's
Which is the most stable?
This is a pragmatic judgement. Parameters might include
- how stable over scale (length)
- amplitude (value or level)
- a vector of amplitude over scale
- proximity to others
So far maxima. What about minima and more?
The filter (sieve) that finds maxima is a connect-set opening ('o' sieve). A 'c' sieve finds the connected-set closing, or minima. To work with minima we could:
- invert the signal, process it, and invert it back.
- OR, in this case, we could substitute a min for a max within SIVND_m.
YY=ones([length(X),1+maxscale]);
for scale=0:maxscale
Y2=SIVND_m(X,scale,'c',1,'l',4);
YY(:,scale+1)=Y2';
Y1=Y2; % each stage of the filter (sieve) is idempotent
end
g=SIVND_m(X,maxscale,'c',1,'g',4);
This implementation also maintains lists of both maxima and minima throughout because there can be value in using the combined operators M, N, m
switch type
case {'o'} % opening, merge all maximal runs of less than scale with their nearest value
data=ND_connected_set_merging(data,scale,type,verbose);
case {'c'} % closing, merge all minima runs of less than scale with their nearest value
data=ND_connected_set_merging(data,scale,type,verbose);
case {'C'} % closing, invert-open-invert
data.workArray=uint8(-double(data.workArray)+256);
data.value=uint8(-double(data.value)+256);
data=ND_connected_set_merging(data,scale,'o',verbose);
data.workArray=uint8(-double(data.workArray)+256);
data.value=uint8(-double(data.value)+256);
case 'M' % Open close
data=ND_connected_set_merging(data,scale,'o',verbose);
data=ND_connected_set_merging(data,scale,'c',verbose);
case 'N' % Close open
data=ND_connected_set_merging(data,scale,'c',verbose);
data=ND_connected_set_merging(data,scale,'o',verbose);
case 'm' % recursive median
data=ND_connected_set_rmedian(data,scale,'m',verbose);
otherwise
error('type not recognised it should be (m, o, c, C, M or N)');
end