One dimensional sieve applied to images: Difference between revisions
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
=<span style="color:Chocolate">Filter</span>= | =<span style="color:Chocolate">Filter</span>= | ||
====<span style="color:SaddleBrown"> | ====<span style="color:SaddleBrown">Lowpass siv4.mex</span>==== | ||
{| border="0" cellpadding="5" cellspacing="5" | {| border="0" cellpadding="5" cellspacing="5" | ||
|- valign="top" | |- valign="top" | ||
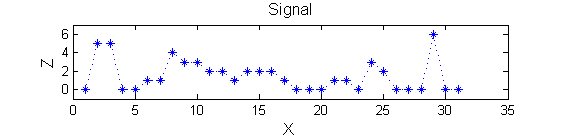
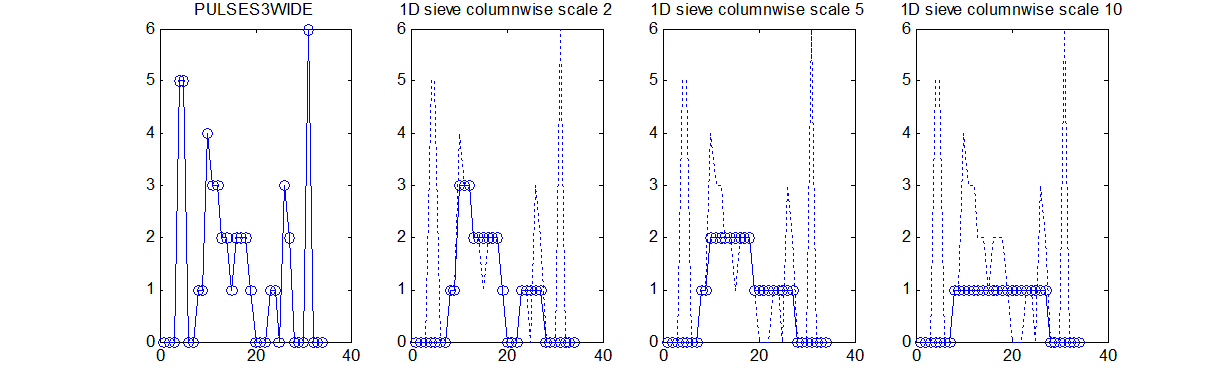
|width="30%"| Imagine that there is a signal, which may comprise positive or negative pulses, that is contaminated by smaller scale noise (leftmost panel). 'siv4.mex' (i.e. compiled from the 'C' to suite your operating system) can filter out the smaller scale noise - irrespective of amplitude. The rightmost panels show the results of removing all 'noise' less than | |width="30%"| Imagine that within the data above there is a signal, which may comprise positive or negative pulses, that is contaminated by smaller scale noise (leftmost panel). 'siv4.mex' (i.e. compiled from the 'C' to suite your operating system) can filter out the smaller scale noise - irrespective of amplitude. The rightmost panels show the results of removing all 'noise' less than scales 1, 5 and 10. Unlike linear filters edges remain well defined and 'noise' is completely removed. | ||
|[[Image:siv4_test_2.png|550px|Sieved]] | |[[Image:siv4_test_2.png|550px|Sieved]] | ||
|} | |} | ||
| Line 27: | Line 27: | ||
ans = | ans = | ||
y: {[34x1 double] [34x1 double] [34x1 double]} % outputs for the 3 specified scales | y: {[34x1 double] [34x1 double] [34x1 double]} % outputs for the 3 specified scales | ||
scan: [34 34] | scan: [34 34] % instructing single column processing | ||
X: [34x1 double] | X: [34x1 double] % input data | ||
options: [3x4 double] | options: [3x4 double] % options (see elsewhere) | ||
outputs: 'lll' | outputs: 'lll' % outputs all lowpass | ||
type: 'int' | type: 'int' % input data may be double but only contains integers | ||
name: 'PULSES3WIDE' | name: 'PULSES3WIDE' | ||
Revision as of 14:17, 18 June 2014
'siv4.mex' implemenation applies the m-sieve column wise
A Matlab function siv4_test.m illustrates how siv4.mex can be used to analyse columns of 1D data.
Consider a signal, <math>X</math>X=getData('PULSES3WIDE')
>blue X=0 5 5 0 0 1 1 4 3 3 2 2 1 2 2 2 1 0 0 0 1 1 0 3 2 0 0 0 6 0 0
|
Filter
Lowpass siv4.mex
data{1}=siv4_alt('PULSES3WIDE',[2;5;10]);
data{1}
ans =
y: {[34x1 double] [34x1 double] [34x1 double]} % outputs for the 3 specified scales
scan: [34 34] % instructing single column processing
X: [34x1 double] % input data
options: [3x4 double] % options (see elsewhere)
outputs: 'lll' % outputs all lowpass
type: 'int' % input data may be double but only contains integers
name: 'PULSES3WIDE'
Non-linear: the starting point for MSER's
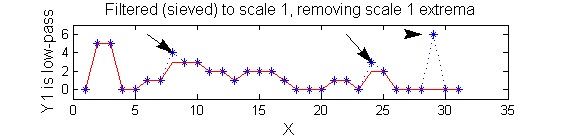
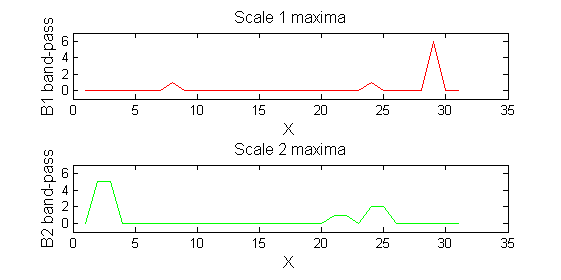
scaleA=1; Y1=SIVND_m(X,scaleA,'o');
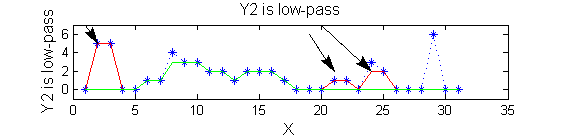
scaleB=2; Y2=SIVND_m(X,scaleB,'o');
red=double(X)-double(Y1); green=double(Y1)-double(Y2);
Repeat over scales 0 to 15
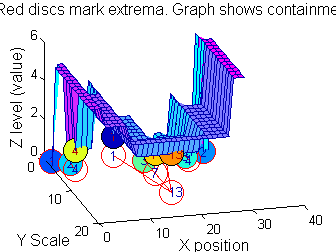
| Increasing the scale (towards the front) removes extrema of increasing length. The algorithm cannot create new maxima (it is an 'o' sieve) it is, therefore, scale-space preserving. | 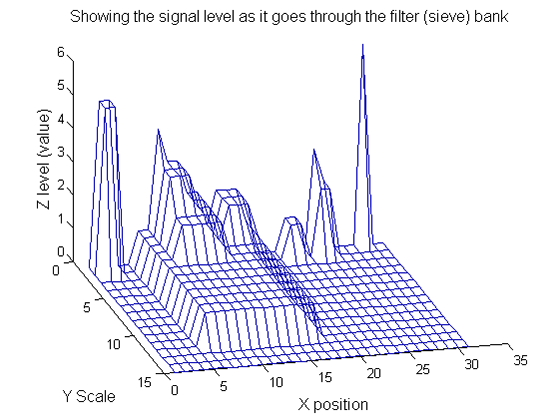
|
YY=ones([length(X),1+maxscale]);
for scale=0:maxscale
Y2=SIVND_m(Y1,scale,'o',1,'l',4);
YY(:,scale+1)=Y2';
Y1=Y2; % each stage of the filter (sieve) is idempotent
end
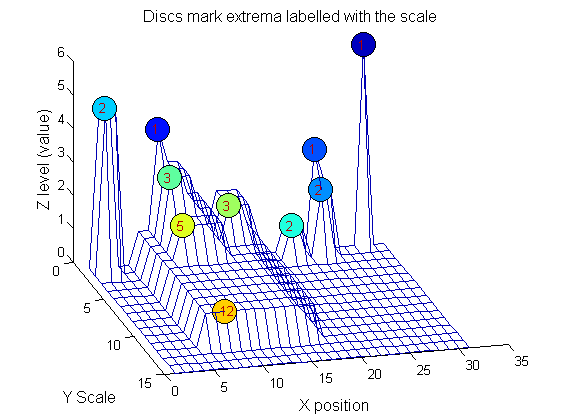
Label the granules
g=SIVND_m(X,maxscale,'o',1,'g',4);
g = Number: 10
area: [1 1 1 2 2 2 3 3 5 12]
value: [6 1 1 2 5 1 1 1 1 1]
level: [6 4 3 2 5 1 3 2 2 1]
deltaArea: [5 2 1 7 3 12 2 2 7 19]
last_area: [6 3 2 9 5 14 5 5 12 31]
root: [29 8 24 24 2 21 8 14 8 8]
PictureElement: {1x10 cell}
g.PictureElement
Columns 1 through 9
[29] [8] [24] [2x1 double] [2x1 double] [2x1 double] [3x1 double] [3x1 double] [5x1 double] [12x1 double]
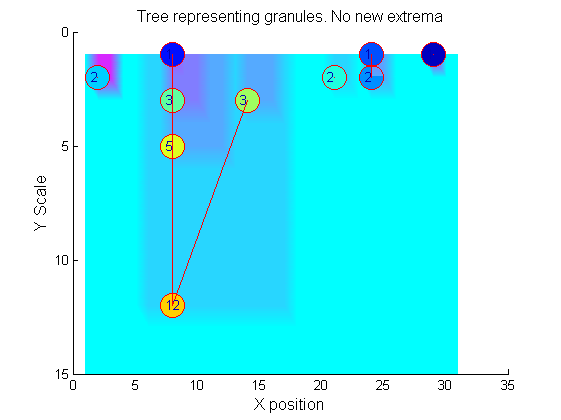
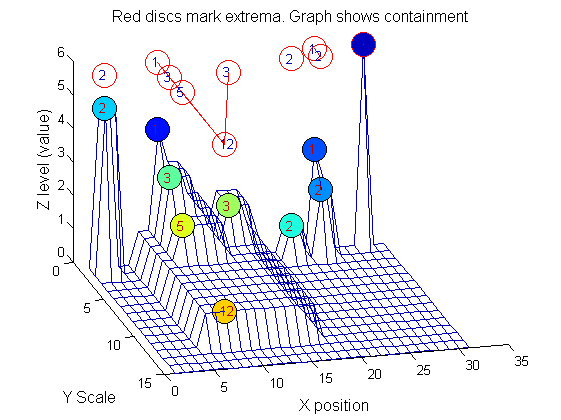
Tracing the granules through scale-space identifies candidate MSER's
We have candidate 1D MSER's
Which is the most stable?
This is a pragmatic judgement. Parameters might include
- how stable over scale (length)
- amplitude (value or level)
- a vector of amplitude over scale
- proximity to others
So far maxima. What about minima and more?
The filter (sieve) that finds maxima is a connect-set opening ('o' sieve). A 'c' sieve finds the connected-set closing, or minima. To work with minima we could:
- invert the signal, process it, and invert it back.
- OR, in this case, we could substitute a min for a max within SIVND_m.
YY=ones([length(X),1+maxscale]);
for scale=0:maxscale
Y2=SIVND_m(X,scale,'c',1,'l',4);
YY(:,scale+1)=Y2';
Y1=Y2; % each stage of the filter (sieve) is idempotent
end
g=SIVND_m(X,maxscale,'c',1,'g',4);
This implementation also maintains lists of both maxima and minima throughout because there can be value in using the combined operators M, N, m
switch type
case {'o'} % opening, merge all maximal runs of less than scale with their nearest value
data=ND_connected_set_merging(data,scale,type,verbose);
case {'c'} % closing, merge all minima runs of less than scale with their nearest value
data=ND_connected_set_merging(data,scale,type,verbose);
case {'C'} % closing, invert-open-invert
data.workArray=uint8(-double(data.workArray)+256);
data.value=uint8(-double(data.value)+256);
data=ND_connected_set_merging(data,scale,'o',verbose);
data.workArray=uint8(-double(data.workArray)+256);
data.value=uint8(-double(data.value)+256);
case 'M' % Open close
data=ND_connected_set_merging(data,scale,'o',verbose);
data=ND_connected_set_merging(data,scale,'c',verbose);
case 'N' % Close open
data=ND_connected_set_merging(data,scale,'c',verbose);
data=ND_connected_set_merging(data,scale,'o',verbose);
case 'm' % recursive median
data=ND_connected_set_rmedian(data,scale,'m',verbose);
otherwise
error('type not recognised it should be (m, o, c, C, M or N)');
end