One dimensional sieve introduction: Difference between revisions
Jump to navigation
Jump to search
| Line 43: | Line 43: | ||
{| border="0" cellpadding="5" cellspacing="5" | {| border="0" cellpadding="5" cellspacing="5" | ||
|- valign="top" | |- valign="top" | ||
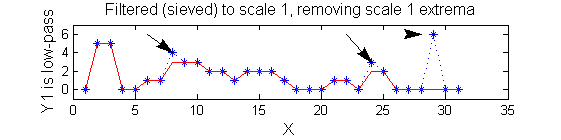
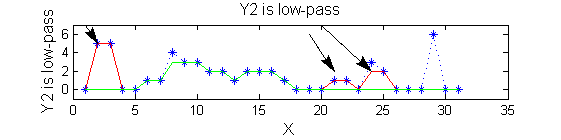
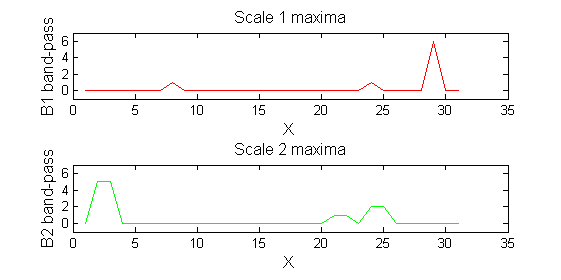
|width="50%"| '''A high-pass''' 'o' sieve scale 1 shows the extrema that have been removed. In red the scale 1 extrema at <math>M^1_8</math> , <math>M^1_{24}</math> , <math>M^1_{29}</math> have been removed. In green extrema of scale 2 are shown. ''In the sieve terminology these are granules.'' Think of grading gravel using sieves, large holes let through large grains and small holes let through small grains. Here scale is measured as length. | |width="50%"| '''A high-pass''' 'o' sieve scale 1 shows the extrema that have been removed. In red the scale 1 extrema at <math>M^1_8</math> , <math>M^1_{24}</math> , <math>M^1_{29}</math> have been removed. In green extrema of scale 2 are shown. ''In the sieve terminology these are granules.'' Think of grading gravel using sieves, large holes let through large grains and small holes let through small grains. Here scale is measured as length. If granules don't fit they don't get through - unlike linear filters which leak. | ||
|[[Image:IllustrateSIV_1_05.png|400px|'o' non-linear filter (sieve)]] | |[[Image:IllustrateSIV_1_05.png|400px|'o' non-linear filter (sieve)]] | ||
|} | |} | ||
Revision as of 10:58, 15 November 2013
1D Signals to MSERs and granules
Matlab function IllustrateSIV_1 illustrates how MSERs (maximally stable extremal regions) and sieves are related. We start with one dimensional signals before moving to two dimensional images and three dimensional volumes.

|
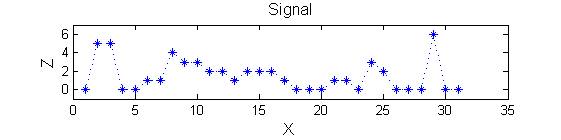
Consider a signal, <math>X</math>X=getData('PULSES3WIDE')
>blue X=0 5 5 0 0 1 1 4 3 3 2 2 1 2 2 2 1 0 0 0 1 1 0 3 2 0 0 0 6 0 0
|
Filter
Linear
| A linear Gaussian filter with <math>\sigma=2</math> attenuates extrema without introducing new ones. But blurring may be a problem. | 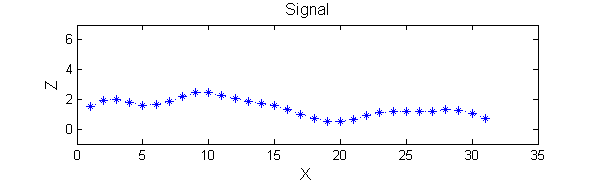
|
h=fspecial('Gaussian',9,2);
Y=conv(X,(h(5,:)/sum(h(5,:))),'same');
Non-linear
scaleA=1; Y1=SIVND_m(X,scaleA,'o');
scaleB=2; Y2=SIVND_m(X,scaleB,'o');