One dimensional sieve introduction: Difference between revisions
Jump to navigation
Jump to search
| Line 31: | Line 31: | ||
|[[Image:IllustrateSIV_1_03.png|400px|'o' non-linear filter (sieve)]] | |[[Image:IllustrateSIV_1_03.png|400px|'o' non-linear filter (sieve)]] | ||
|} | |} | ||
scaleA=1; | |||
Y1=SIVND_m(X,scaleA,'o'); | |||
{| border="0" cellpadding="5" cellspacing="5" | {| border="0" cellpadding="5" cellspacing="5" | ||
|- valign="top" | |- valign="top" | ||
| Line 36: | Line 38: | ||
|[[Image:IllustrateSIV_1_04.png|400px|'o' non-linear filter (sieve)]] | |[[Image:IllustrateSIV_1_04.png|400px|'o' non-linear filter (sieve)]] | ||
|} | |} | ||
scaleB=2; | |||
Y2=SIVND_m(X,scaleB,'o'); | |||
Revision as of 10:08, 15 November 2013
1D Signals
Matlab function IllustrateSIV_1 illustrates how MSERs (maximally stable extremal regions) and sieves are related. We start with one dimensional signals before moving to two dimensional images and three dimensional volumes.
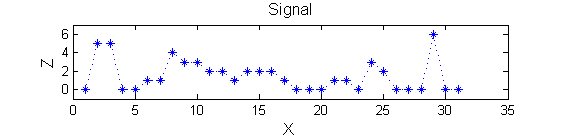
| Consider a signal, <math>X</math> X=getData('PULSES3WIDE') |
Filter
Linear
| A linear Gaussian filter with <math>\sigma=2</math> attenuates extrema without introducing new ones. But blurring may be a problem. | 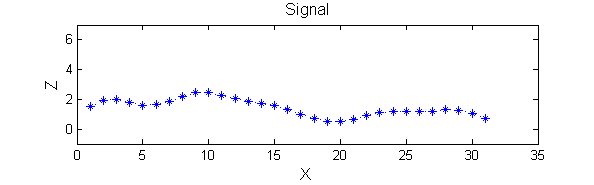
|
h=fspecial('Gaussian',9,2);
Y=conv(X,(h(5,:)/sum(h(5,:))),'same');
Non-linear
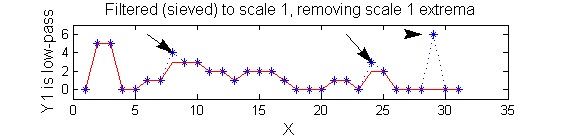
scaleA=1; Y1=SIVND_m(X,scaleA,'o');
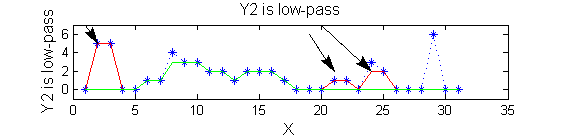
scaleB=2; Y2=SIVND_m(X,scaleB,'o');