One dimensional sieve introduction: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 11: | Line 11: | ||
{| border="0" cellpadding="5" cellspacing="5" | {| border="0" cellpadding="5" cellspacing="5" | ||
|- valign="top" | |- valign="top" | ||
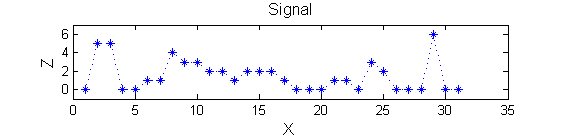
[[Image:IllustrateSIV_1_02.png| | |width="50%"| <math>X</math> has three one-sample-wide maxima (<math>M^1_8</math> , <math>M^1_{24}</math> , <math>M^1_{29}</math> ), two two-sample-wide maxima (<math>M^2_{14}</math> , <math>M^2_{21}</math>) some of which, when removed, will persist as larger scale maxima, e.g. <math>M^1_{24}</math> will become two samples wide as the peak is clipped off. | ||
|[[Image:IllustrateSIV_1_02.png|400px]] | |||
|} | |} | ||
=<span style="color:Chocolate">Filter</span>= | =<span style="color:Chocolate">Filter</span>= | ||
====Linear==== | |||
{| border="0" cellpadding="5" cellspacing="5" | |||
|- valign="top" | |||
|width="50%"| A linear Gaussian filter with <math>\sigma=2</math> attenuates extrema without introducing new ones. But blurring may be a problem. | |||
|[[Image:GaussianSmoothedSigma2.png|350px|Gaussian filtered]] | |||
|} | |||
====Non-linear==== | |||
{| border="0" cellpadding="5" cellspacing="5" | |||
|- valign="top" | |||
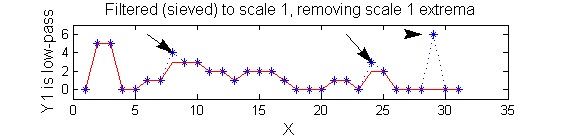
|width="50%"| A low-pass 'o' sieve scale 1 (non-linear filter underpinning the MSER algorithm) can remove scale 1 maxima. The result is shown in red, extrema at <math>M^1_8</math> , <math>M^1_{24}</math> , <math>M^1_{29}</math> have been removed. There is no blur. The remaining signal is unchanged. | |||
|[[Image:IllustrateSIV_1_03.png|400px|'o' non-linear filter (sieve)]] | |||
|} | |||
{| border="0" cellpadding="5" cellspacing="5" | |||
|- valign="top" | |||
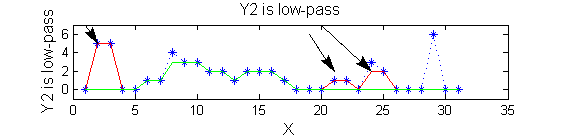
|width="50%"| Scale 2 maxima are removed next using the 'o' sieve scale 2. The result is shown in green. Extrema at <math>M^2_{14}</math> , <math>M^2_{21}</math> have been removed. Still no blur and what remains is unchanged. | |||
|[[Image:IllustrateSIV_1_04.png|400px|'o' non-linear filter (sieve)]] | |||
|} | |||
Revision as of 21:16, 14 November 2013
1D Signals
Matlab function IllustrateSIV_1 illustrates how MSERs (maximally stable extremal regions) and sieves are related. We start with one dimensional signals before moving to two dimensional images and three dimensional volumes.
| Consider a signal, <math>X</math> X=getData('PULSES3WIDE') |
Filter
Linear
| A linear Gaussian filter with <math>\sigma=2</math> attenuates extrema without introducing new ones. But blurring may be a problem. | 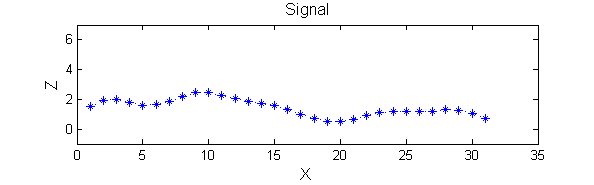
|