Main Page: Difference between revisions
No edit summary |
No edit summary |
||
| Line 90: | Line 90: | ||
|} | |} | ||
<br> | <br> | ||
In development. | |||
Revision as of 05:51, 3 July 2013
Bangham at UEA
Bangham Lab - Home
Current activity: a collaboration with the CoenLab with the aim of understanding how patterns of gene activity in biological organs influence the developing shape. The BanghamLab is focussed on the conceptual underpinning: concepts captured in computational growth models, experimental data visualisation and analysis.
Computational biology toolboxes
Growing complex biological shapes from patterns of gene expression
Movies: Model Snapdragon flower movie, Why Snapdragon flower shape is so complex
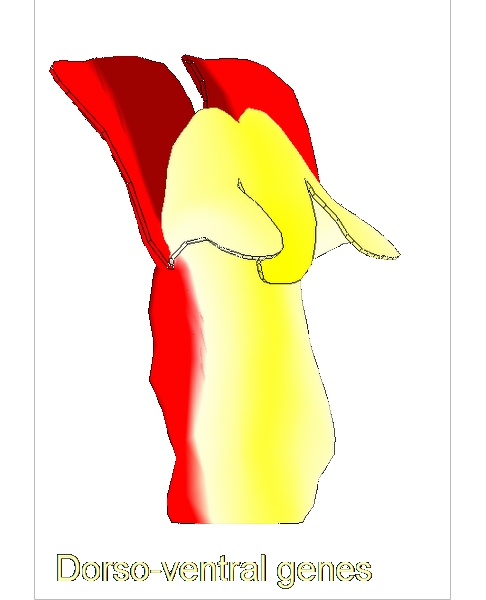
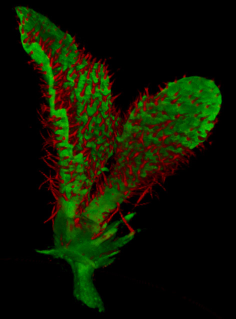
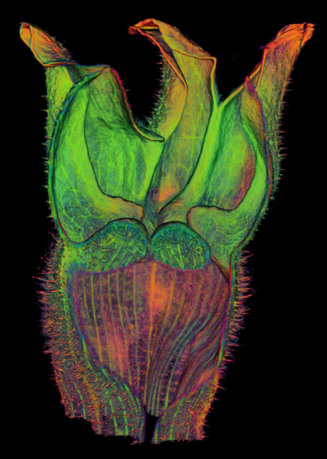
The growth of a complex snapdragon flower shape. Key to the model, is an hypothesis on how organisers control the axes along which growth occurs. The organisers are shown in cyan and green. On the right are the shapes of two symmetrical mutants computed from the same model (hypotheses).
The Growing Polarised Tissue Framework for understanding and modelling the relationship between gene activity and the growth of shapes such leaves, flowers and animal embryos is introduced in (Kennaway et al 2011). The GPT-framework was used to capture an understanding of (to model) the Snapdragon flower Green et al 2011. The Snapdragon model was validated by comparing the results with other mutant and transgenic flowers Cui et al 2010.
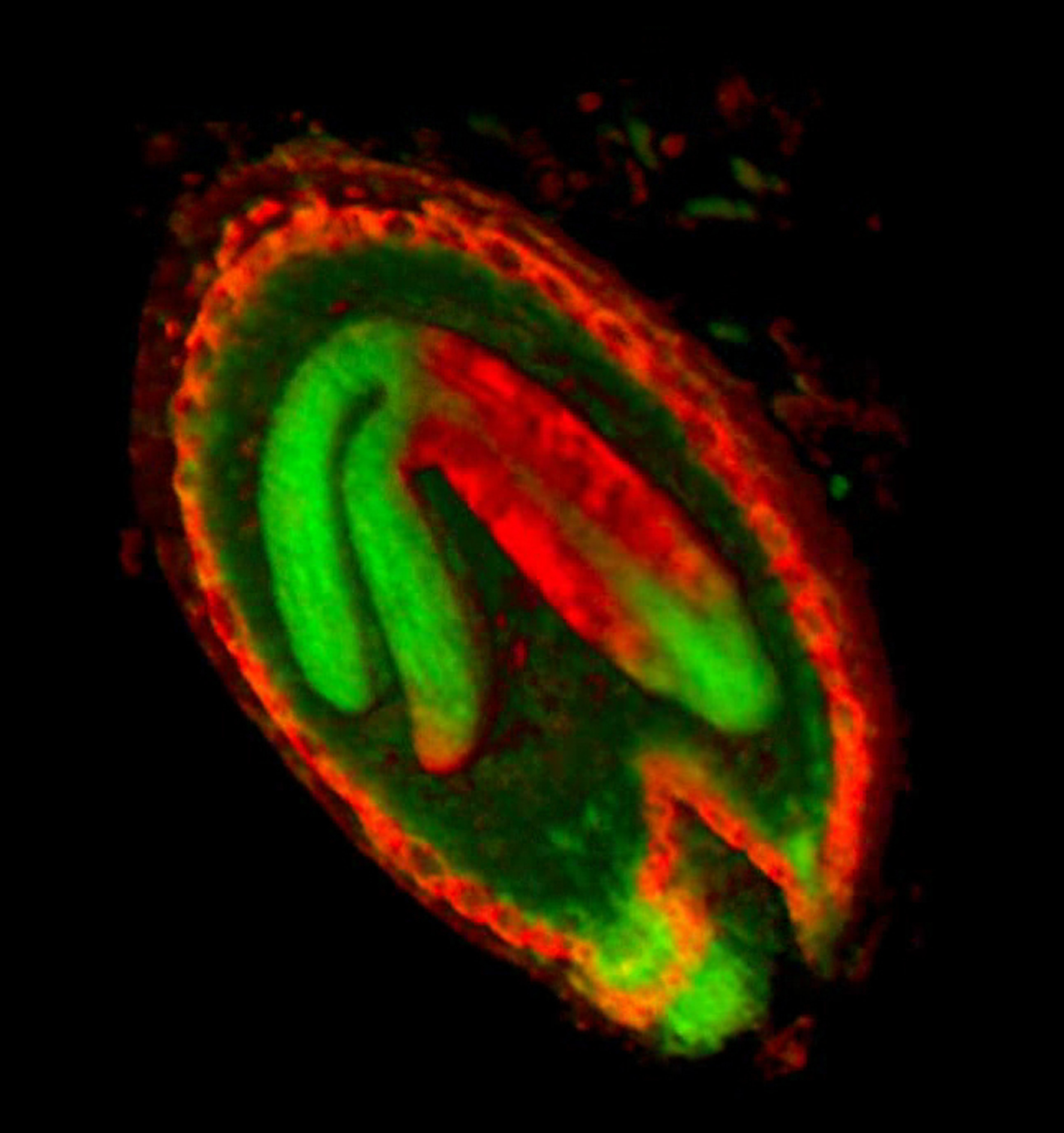
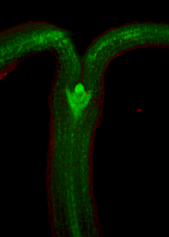
The GPT-framework was also used to model the developing shape of Arabidopsis leaves as they grow (Kuchen et al 2012) a model that was extended to include Arabidopsis petals Sauret-Güeto et al 2013.
Viewing three dimensional images
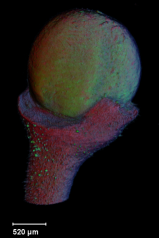
Images of plants, plant organs and cells.
VolViewer uses OpenGL and Qt to provide a user friendly application to interactively explore and quantify multi-dimensional biological images. It has been successfully used in our lab to explore and quantify confocal microscopy and optical projection tomography images. It is open-source and is compatible with the Open Microscopy Environment (OME).
Movies of carnivorous plants
More details on viewing three dimensional images
Analysing shapes: faces, leaves and flowers

MORE
Seen the origional paintings? Do they exist?.
The AAMToolbox is used to analyse the shape and colour of collections of similar objects. Originally developed to analyse face shapes for lipreading (Matthews et al. 2002version of pdf), we have used it extensively for analysing the shapes of leaves (Langlade et al 2005.,Bensmihen et al. 2010) and petals (Whibley et al 2006,Feng et al. 2010). The analysis can be applied to art, for example, finding systematic differences between portraits by Rembrandt and Modigliani.
More details on analysing shapes
Algorithms
Reaction-diffusion and morphogenesis - the growth of shapes
MORE
In 1952 Alan Turing proposed The chemical basis of Morphogenesis - "... suggested that a system of chemical substances, called morphogens, reacting together and diffusing through a tissue, is adequate to account for the main phenomena of morphogenesis. Such a system, although it may originally be quite homogeneous, may later develop a pattern or structure due to an instability of the homogeneous equilibrium, which is triggered off by random disturbances. ..." Such patterning is now widely known. However, the morphogenesis element of the story has been less widely explored - here we illustrate the process using GFtbox - but also see: plant meristemreview related plant stuff
Two chemical substances react and diffuse to dynamically develop a pattern of spots (top row). We have added two simple growth rules (based on our hypotheses on the growth of shapes) to dynamically translate the pattern into a pattern of growth (bottom row). The changing geometry arising through growth which in turn feeds back on the reaction-diffusion system to modulate patterning. One of the morphogenesis rules uses the chemical concentration gradient to set the axes for anisotropic growth (arrows in third panel).
This model was featured in a video interview exhibit in the London Science Museum 'Codebreakers' exhibition Codebreakers.
More details on reaction-diffusion and morphogenesis
MSER's, extrema, Connected-set filters, Sieves and Scale-space
In development.