One dimensional sieve applied to images: Difference between revisions

From BanghamLab
Jump to navigation Jump to search
 
(8 intermediate revisions by the same user not shown)
Line 35: Line 35:
       name: 'PULSES3WIDE'
       name: 'PULSES3WIDE'


====<span style="color:navy">Now think about '''scale-space'''. </span>====
====<span style="color:navy">Now what about '''scale-space'''?. </span>====
[[Image:Siv4 test 5.png|500px|center|'m' non-linear filter (sieve) compared to Gaussian filter]]
[[Image:Siv4 test 5.png|400px|center|'m' non-linear filter (sieve) compared to Gaussian filter]]
{| border="0" cellpadding="5" cellspacing="5"
{| border="0" cellpadding="5" cellspacing="5"
|- valign="top"
|- valign="top"
Line 42: Line 42:
The 'm'-sieve preserves scale-space so no new extrema (light regions) are formed as we move to increasing scales.<br>
The 'm'-sieve preserves scale-space so no new extrema (light regions) are formed as we move to increasing scales.<br>
|width="50%"| Right Panel. A ''Gaussian'' filter bank also preserves scale-space as shown by Witkin 1986.<br>
|width="50%"| Right Panel. A ''Gaussian'' filter bank also preserves scale-space as shown by Witkin 1986.<br>
(Babaud et. al. 1986 "The uniqueness of the Gaussian kernel ...")<ref>Babaud, Jean; Witkin, Andrew P.; Baudin, Michel; Duda, Richard O., "Uniqueness of the Gaussian Kernel for Scale-Space Filtering," Pattern Analysis and Machine Intelligence, IEEE Transactions on , vol.PAMI-8, no.1, pp.26,33, Jan. 1986 doi: 10.1109/TPAMI.1986.4767749</ref>
(Babaud et. al. 1986 "The uniqueness of the Gaussian kernel ...")<ref>Babaud, Jean; Witkin, Andrew P.; Baudin, Michel; Duda, Richard O., "Uniqueness of the Gaussian Kernel for Scale-Space Filtering," Pattern Analysis and Machine Intelligence, IEEE Transactions on , vol.PAMI-8, no.1, pp.26,33, Jan. 1986 doi: 10.1109/TPAMI.1986.4767749</ref>==References==
<references />
 
|}
|}


====<span style="color:navy">Using ''granules'' to represent the data segment. </span>====
{| border="0" cellpadding="5" cellspacing="5"
{| border="0" cellpadding="5" cellspacing="5"
|- valign="top"
|- valign="top"
|width="50%"| Another heat-map. The plot is an alternative view of the left Panel above. This time showing the features (at each scale) that are peeled off (removed) by increasing scale sieve filters.  The color map is 'jet' to make the features, we call them granules, more obvious. It is possible to imagine a 'tree' representation of these granules.  
|width="50%"| Another heat-map. The plot is an alternative view of the left Panel above. This time showing the features (at each scale) that are peeled off (removed) by increasing scale sieve filters.  The color map is 'jet' to make the features more visible. We call these features granules. Granules are a mapping of the original signal. Thus, the granularity domain contains all the information in the original signal. It is possible to imagine a 'tree' representation of these granules and then use some mechanism to select 'salient' granules (features). ([[One_dimensional_sieve_introduction#Tracing_the_granules_through_scale-space_identifies_candidate_MSER.27s | see here for the connection with MSER's.]]) The idea is to 'concentrate' the useful information.
|width="50%"| [[Image:Siv4 test granules.png|400px|'o' non-linear filter (sieve)]]
|width="50%"| [[Image:Siv4 test granules.png|400px|'o' non-linear filter (sieve)]]
|}
|}
 
An alternative is to treat the granularity domain in the manner of wavelets and concentrate the useful information by summing the 'energy' within the granules (in the signal fragment) along each scale to produce a histogram the equivalent of a local power spectrum. This can be further simplified into, say, twenty logarithmically spaced scale-bands. These two steps lose information (but hopefully concentrate useful components). To be useful, granularity spectrum should be normalised. One way is to compute the equivalent of the cepstrum. Similarly, the phase.
====<span style="color:SaddleBrown">Repeat over scales 0 to 15</span>====
{| border="0" cellpadding="5" cellspacing="5"
|- valign="top"
|width="50%"| Increasing the scale (towards the front) removes extrema of increasing length. The algorithm cannot create new maxima (it is an 'o' sieve) it is, therefore, scale-space preserving.
|[[Image:Replacement IllustrateSIV 1 07.png|400px|'o' non-linear filter (sieve)]]
|}
YY=ones([length(X),1+maxscale]);
for scale=0:maxscale
    Y2=SIVND_m(Y1,scale,'o',1,'l',4);
    YY(:,scale+1)=Y2';
    Y1=Y2; <span style="color: Green">% each stage of the filter (sieve) is idempotent</span>
end
 
====<span style="color:SaddleBrown">Label the granules</span>====
{| border="0" cellpadding="5" cellspacing="5"
|- valign="top"
|width="50%"|We can create a data structure that captures the properties of each granule. The number in each disc indicates the granule scale.  Each cell in the PictureElement field has a list of indexes recording the granule position (<math>X</math>). (In 1D this is best done run-length coded but this code is designed to also work in 2D.)
|[[Image:IllustrateSIV_1_08.png|400px|'o' non-linear filter (sieve)]]
|}
g=SIVND_m(X,maxscale,'o',1,'g',4);
g =  Number: 10
              area: [1 1 1 2 2 2 3 3 5 12]
            value: [6 1 1 2 5 1 1 1 1 1]
            level: [6 4 3 2 5 1 3 2 2 1]
        deltaArea: [5 2 1 7 3 12 2 2 7 19]
        last_area: [6 3 2 9 5 14 5 5 12 31]
              root: [29 8 24 24 2 21 8 14 8 8]
    PictureElement: {1x10 cell}
 
g.PictureElement
 
  Columns 1 through 9
 
    [29]    [8]    [24]    [2x1 double]    [2x1 double]    [2x1 double]    [3x1 double]    [3x1 double]    [5x1 double]  [12x1 double]
 
====<span style="color:SaddleBrown">Tracing the granules through scale-space identifies candidate MSER's</span>====
{| border="0" cellpadding="5" cellspacing="5"
|- valign="top"
|width="50%"|The granules contain all the information in the signal. The tree illustrates the relationship between granules. The granules at <math>X=8</math> (scales 1, 3, 5, 12) indicates a region that is stable over scale. Likewise at <math>X=24</math> (scales 1, 2). One might argue that the latter is the less stable.
[[Image:IllustrateSIV_1_10.png|250px|'o' non-linear filter (sieve)]]
 
|[[Image:IllustrateSIV_1_09.png|400px|'o' non-linear filter (sieve)]]
|}
 
=<span style="color:Chocolate">We have candidate 1D MSER's</span>=
<span style="color:SaddleBrown">'''Which is the ''most stable''?'''<br><br>
This is a pragmatic judgement. Parameters might include</span>
#<span style="color:SaddleBrown">how stable over scale (length)</span>
#<span style="color:SaddleBrown">amplitude (value or level)</span>
#<span style="color:SaddleBrown">a vector of amplitude over scale</span>
#<span style="color:SaddleBrown">proximity to others</span>
 
=<span style="color:Chocolate">So far '''''maxima'''''. What about ''minima'' and more?</span>=
The filter (sieve) that finds maxima is a connect-set ''opening'' ('o' sieve). A 'c' sieve finds the connected-set closing, or minima. To work with minima we could:
*invert the signal, process it, and invert it back.
*OR, in this case, we could substitute a min for a max within SIVND_m.  
YY=ones([length(X),1+maxscale]);
for scale=0:maxscale
    Y2=SIVND_m(X,scale,'c',1,'l',4);
    YY(:,scale+1)=Y2';
    Y1=Y2; % each stage of the filter (sieve) is idempotent
end
g=SIVND_m(X,maxscale,'c',1,'g',4);
{| border="0" cellpadding="5" cellspacing="5"
|- valign="top"
|width="50%"|Closing sieve 'c' sieve. To make it clearer the 'FaceColor' is 'flat' and the graph is placed at the bottom. To find minima at ALL scales it would be necessary to go to scales greater than 15.<br><br>
<span style="color:Chocolate">'''Which is better for finding 1D MSER's, 'o' or 'c'?'''</span>
*It depends on the data
*Further alternative operators include 'M', 'N' and 'm' which might be better still (to be discussed elsewhere).
|[[Image:Illustrate_c_SIV_1_09.png|400px|'o' non-linear filter (sieve)]]
|}
 
 
This implementation also maintains ''lists of both maxima and minima'' throughout because there can be value in using the combined operators M, N, m
        switch type
            case {'o'} % opening, merge all maximal runs of less than scale with their nearest value
                data=ND_connected_set_merging(data,scale,type,verbose);
            case {'c'} % closing, merge all minima runs of less than scale with their nearest value
                data=ND_connected_set_merging(data,scale,type,verbose);
            case {'C'} % closing, invert-open-invert
                data.workArray=uint8(-double(data.workArray)+256);
                data.value=uint8(-double(data.value)+256);
                data=ND_connected_set_merging(data,scale,'o',verbose);
                data.workArray=uint8(-double(data.workArray)+256);
                data.value=uint8(-double(data.value)+256);
            case 'M' % Open close
                data=ND_connected_set_merging(data,scale,'o',verbose);
                data=ND_connected_set_merging(data,scale,'c',verbose);
            case 'N' % Close open
                data=ND_connected_set_merging(data,scale,'c',verbose);
                data=ND_connected_set_merging(data,scale,'o',verbose);
            case 'm' % recursive median
                data=ND_connected_set_rmedian(data,scale,'m',verbose);
            otherwise
                error('type not recognised it should be (m, o, c, C, M or N)');
        end

Latest revision as of 21:55, 22 June 2014

Return to MSERs and extrema

'siv4.mex' implemenation applies the m-sieve to a vector or column wise to a matrix

A Matlab function siv4_test.m illustrates how siv4.mex can be used to analyse columns of 1D data.

Consider a signal, <math>X</math>
X=getData('PULSES3WIDE')
>blue  X=0 5 5 0 0 1 1 4 3 3 2 2 1 2 2 2 1 0 0 0 1 1 0 3 2 0 0 0 6 0 0
The data has minima and maxima of different scales (lengths). In one dimension we measure pulse length using a ruler, measuring tape or whatever - but not frequency or Gaussian scale. 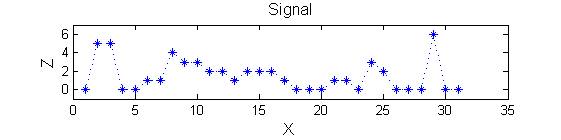IllustrateSIV 1 02.png

Filter

Lowpass siv4.mex

Imagine that within the data above there is a signal, which may comprise positive or negative pulses, that is contaminated by smaller scale noise (leftmost panel).

Then 'siv4.mex' (i.e. compiled from the 'C' to suite your operating system) can filter out the smaller scale noise - irrespective of amplitude, i.e. it removes smaller scale (length) extrema.

The rightmost panels show the results of removing all 'noise' less than scales 1, 5 and 10. Unlike linear filters edges remain well defined and 'noise' is completely removed.

Sieved 
data{1}=siv4_alt('PULSES3WIDE',[2;5;10]);
data{1}
       ans = 
         y: {[34x1 double]  [34x1 double]  [34x1 double]} % outputs for the 3 specified scales
      scan: [34 34]            % instructing single column processing
         X: [34x1 double]    % input data
   options: [3x4 double]   % options (see elsewhere)
   outputs: 'lll'                 % outputs all lowpass
      type: 'int'                 % input data may be double but only contains integers
      name: 'PULSES3WIDE'

Now what about scale-space?.

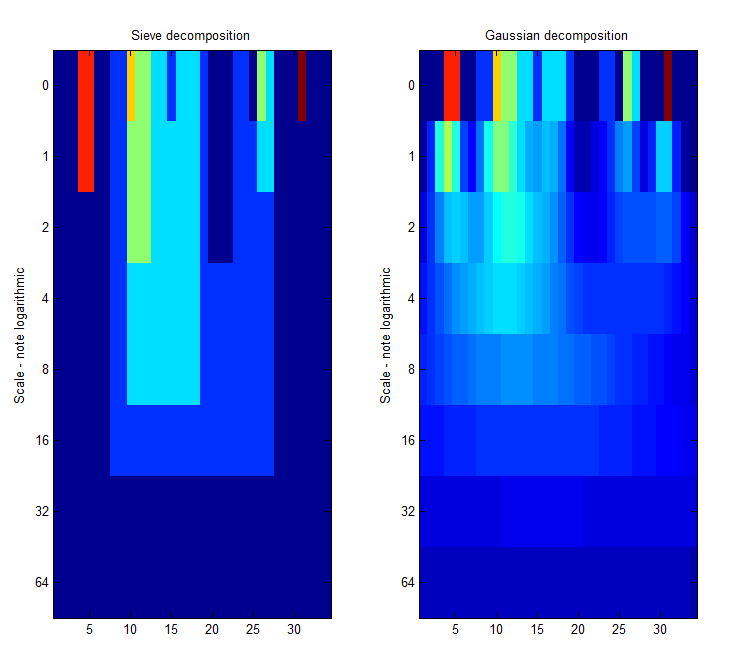
'm' non-linear filter (sieve) compared to Gaussian filter
Left Panel. A low-pass 'm' sieve can remove extrema at multiple scales. Here, siv4.m gradually removes extrema as scale increases from scale 1 to scale 64. The resulting traces are shown as a 'heat map' where the signal goes from left to right, bright colours like red are large amplitude, small scale extrema. At each increasing scale (down the map) extrema have been removed. As result, we can for example see the buried large scale, low amplitude pulse revealed in panel 4 of the previous Figure, as a light green rectangle that starts at n=6 and persists to n=26, i.e. scale=20.

The 'm'-sieve preserves scale-space so no new extrema (light regions) are formed as we move to increasing scales.

 Right Panel. A Gaussian filter bank also preserves scale-space as shown by Witkin 1986.

(Babaud et. al. 1986 "The uniqueness of the Gaussian kernel ...")<ref>Babaud, Jean; Witkin, Andrew P.; Baudin, Michel; Duda, Richard O., "Uniqueness of the Gaussian Kernel for Scale-Space Filtering," Pattern Analysis and Machine Intelligence, IEEE Transactions on , vol.PAMI-8, no.1, pp.26,33, Jan. 1986 doi: 10.1109/TPAMI.1986.4767749</ref>==References== <references />

Using granules to represent the data segment.

Another heat-map. The plot is an alternative view of the left Panel above. This time showing the features (at each scale) that are peeled off (removed) by increasing scale sieve filters. The color map is 'jet' to make the features more visible. We call these features granules. Granules are a mapping of the original signal. Thus, the granularity domain contains all the information in the original signal. It is possible to imagine a 'tree' representation of these granules and then use some mechanism to select 'salient' granules (features). ( see here for the connection with MSER's.) The idea is to 'concentrate' the useful information. 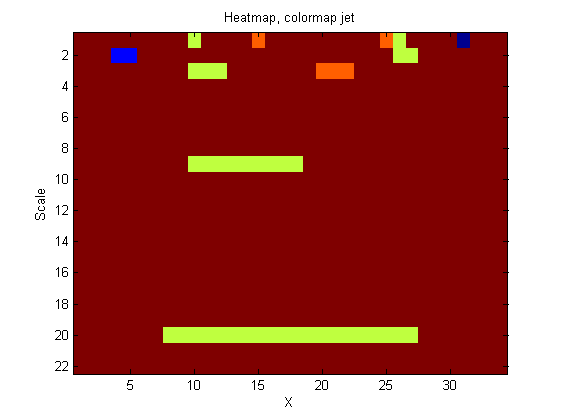'o' non-linear filter (sieve)

An alternative is to treat the granularity domain in the manner of wavelets and concentrate the useful information by summing the 'energy' within the granules (in the signal fragment) along each scale to produce a histogram the equivalent of a local power spectrum. This can be further simplified into, say, twenty logarithmically spaced scale-bands. These two steps lose information (but hopefully concentrate useful components). To be useful, granularity spectrum should be normalised. One way is to compute the equivalent of the cepstrum. Similarly, the phase.

Retrieved from "http://cmpdartsvr3-v.uea.ac.uk/wiki/BanghamLab/index.php?title=One_dimensional_sieve_applied_to_images&oldid=6802"